我們有一些已知長度的金屬棒，請問可以找出所需的特定長度的金屬棒嗎？必要時，可以把幾根金屬棒焊接成更長的一根，但金屬棒不得切割。

Input

輸入的第一行含有一個整數 $t$、$0\leq{t}\leq{50}$，表示測資的筆數。每筆測資三行，第一行有一個數字 $n$、$0\leq{n}\leq{1000}$，表示我們所要的長度。第二行有一個數字 $p$、$1\leq{p}\leq{20}$，表示我們所擁有的金屬棒的數量。第三行有 $p$ 個數字，表示 $p$ 根金屬棒的長度。

Output

每筆測資輸出一行，依是否可能成功輸出 YES 或 NO。

Sample Input

4
25
4
10 12 5 7
925
10
45 15 120 500 235 58 6 12 175 70
120
5
25 25 25 25 25
0
2
13 567

Sample Output

NO
YES
NO
YES

速食店除了提供食物的單點之外，通常也會提供「套餐」的選擇。例如：菜單可能像這樣：

買套餐組合會比各項單獨買來的便宜。(廢話，否則誰會買套餐。)

一個有很多小孩的媽媽面臨了一種情況：比方說，我需要 9 份漢堡，6 份薯條和 8 份爆米花，我要如何從菜單選擇可以買到我所需要的，而且付的錢最少？請注意：我是一個保守主義者，所以我絕不會買比需要多的食物。

Input

輸入含有多筆測資，每筆測資含有菜單及幾個訂單。

1. 菜單：先個別單點，然後是組合套餐。
   1. 個別單點：有一個整數 $I$ ($I\leq{6}$)，然後是各單點的價格 (每項最多 \$10)
   2. 組合套餐：有一個整數代表有多少種組合套餐 (最多 8 種)。接下來就是每種組合套餐的內容：包含各項單點的 $I$ 個數目，然後是價錢。
      以下的 Sample Input 的菜單即是上面所敘述的。
2. 訂單：訂單的數目 (最多 10)，然後是各訂單的內容 ($I$ 個數字代表所需各項目的數量，每個數字最多為 9)

所有的價格均以分 (cent) 為單位。(1 dollar = 100 cent)

Output

對於每筆測資的每個訂單，輸出一列，最少要付多少錢才能買到他所需要的食物。

Sample Input

4 349 99 109 219
2
1 1 1 0 479
2 2 2 1 999
2
9 6 8 0
9 6 8 5

Sample Output

4139
4700

Maya 是一隻愛幫助朋友的蜜蜂。Maya 的好朋友 Willy 是一隻雄蜂。他剛發現他沒有爸爸，他覺得很困擾。

雄蜂 Willy

Maya 知道雌蜂有雙親 (一個爸爸和一個媽媽)，但是雄蜂則只有一個媽媽而沒有爸爸。這是因為未交配的雌蜂所產的卵會孵出雄蜂，但是受精的卵則會孵出雌蜂。

在 Maya 曉以大義之後，Willy 開始好奇他有多少祖先。他有一個媽媽，兩個祖父母 (一個祖父和一個祖母)。他也有三個曾祖父母。因為 Willy 很懶，不想做太多計算，他要請你寫個程式來幫他計算某一代的祖先一共有幾個。假設同一代的祖先之間沒有親戚關係。

Input

你的程式會收到一連串的正整數，一個一行，各自代表一個世代。世代的最大值為 80。輸入以 0 結束。

Output

對於每筆測資，你的程式要印出 Willy 在那個世代有幾個祖先。

Sample Input

1
2
3
0

Sample Output

1
2
3

Erin 是一個開火車工程師。他也安排火車的各個車廂。他喜歡把車廂按照其重量來安排，重的車廂排在前端。

不幸的是，把車廂排序並不是一件容易的事。你無法把一節車廂拿起來，然後放在另一個位置 (真正的火車又不是積木)。也就是說要把一節車廂插在一列現有的火車中間是不可能的。你只能將一節車廂加在一列火車的前端或後端。

各個車廂來到火車站的順序及其重量是已經知道的。當每節車廂來到的時候，Erin 可以把它加到火車的兩端，或者不加進去。最後，火車的總車廂數是越長越好，不過要記得車廂得按照重量大小排列。

給你按照出現順序各車廂的重量，Erin 最長可安排車廂的長度是多少？

Input

輸入的第一列有一個整數表示測試資料的組數。

每組資料的第一列會有 1 個整數 $n$ ($0\leq{n}\leq{2000}$)，代表車廂的數目。接下來 $n$ 列整數，每列有一個大於等於 0 的整數，代表各車廂的重量。請注意：所有車廂的重量都不一樣。請參考 Sample Input。

Output

對每組測試資料，Erin 最長可安排車廂的長度是多少。

Sample Input

2
3
1
2
3
3
1
3
2

Sample Output

3
2

給你一序列 N 個整數，然後在數字之間插入加或減號，這樣可以得到不同的運算結果。例如：給你 4 個整數：17, 5, -21, 15，就會有 8 種不同的結果：

17    +    5    +    -21    +    15    =    16
17    +    5    +    -21    -    15    =    -14
17    +    5    -    -21    +    15    =    58
17    +    5    -    -21    -    15    =    28
17    -    5    +    -21    +    15    =    6
17    -    5    +    -21    -    15    =    -24
17    -    5    -    -21    +    15    =    48
17    -    5    -    -21    -    15    =    18

假如其中任一運算的結果可以被 $K$ 整除，我們稱這一序列的整數是 「可被 K 整除的 (divisible by K)」，在上例中，此一序列可被 $7$ 整除 ($17+5+-21-15=-14$)，但是無法被 $5$ 整除。

你的任務是寫一個程式判斷一序列整數的可整除性。

Input

輸入一開始會有一個整數 $M$ 表示測試資料的組數。

每組資料的第一列會有 2 個整數 $N,K$ ($1\leq{N}\leq{10000}, 2\leq{K}\leq{100}$) 。第二列含有 $N$ 個整數，代表此序列中的 $N$ 個整數。每個數字的大小其絕對值不會超過 $10000$。

Output

對每組測試資料，如果在這 $N$ 個整數之間任意插入 + 或 - 運算的結果可以被 $K$ 整除，請輸出 Divisible，否則請輸出 Not divisible。

Sample Input

2
4 7
17 5 -21 15
4 5
17 5 -21 15

Sample Output

Divisible
Not divisible

John 是一位寶物獵人，他知道附近海域所有沉在海裡的金幣的位置及深度，及其金幣的數量，不過他只帶了一個氧氣桶過來，所需的氧氣量可能不夠讓他將所有的寶物全都打撈上來，請你幫忙計算他最多可帶回多少金幣，需符合下列限制條件：

• 金幣所在 $n$ 個不同的位置，以 $\{(d_1,v_1), (d_2,v_2), \cdots{},(d_n,v_n)\}$ 表示這 $n$ 個位置的 (深度, 金幣的數量)，$n$ 最大為 30。
• 氧氧桶最多可使用 $t$ 秒，$t$ 最多 1000 秒。
• 每一次潛下水面，他可帶回所有沉在該位置的金幣。
• 下沉所需的時間 ${td}_i$ 為 $w\times{d_i}$，$w$ 為一常數。
• 浮起所需的時間 ${ta}_i$ 為 $2w\times{d_i}$，$w$ 為一常數。
• 輸入的所有數值皆為整數。

Input

輸入有多組測試資料，每組資料的第一列有兩個整數分別表示 $t,w$，第二列有一個整數為 $n$，接下來的 $n$ 列，每列有兩個整數分別表示金幣所在的深度 $d_i$ 及數量 $v_i$。

每組測試資料間有一空行隔開。

Output

請在每組測試資料的第一列輸出 John 可找到的所有金幣的數量，第二列輸出共需潛水幾次，之後的每一列輸出每次潛水的深度及帶回的金幣數量，其輸出順序需與輸入資料的金幣出現順序相同。

請在每組輸出資料間以一列空行隔開。

Sample Input

210 4
3
10 5
10 1
7 2

Sample Output

7
2
10 5
7 2

給定一個有 $n$ 個整數的數列 $a_1, a_2, \cdots{}, a_n$，且數列以非遞減的次序排列，並給定多組整數對 $i, j$ ($1\leq{i}\leq{j}\leq{n}$)，請你從 $a_i, \cdots{}, a_j$ 中找出出現次數最多的數值共出現幾次。

Input

輸入有多組測試資料，每組資料的第一列有兩個整數 $n, q$ ($1\leq{n, q}\leq{100000}$)。下一列有 $n$ 個以空白字元隔開的整數 $a_1, a_2, \cdots{}, a_n$ ($-100000\leq{a_i}\leq{100000}$，其中 $i$ 為 $1$ 到 $n$)，接下來有 $q$ 列每列表示一組 $i, j$。

最後一組測試資料以一列一個 0 表示測試資料結束。

Output

請對每次查詢的數對中找出其範圍內同一數值出現最多次的次數。

Sample Input

10 3
-1 -1 1 1 1 1 3 10 10 10
2 3
1 10
5 10
0

Sample Output

1
4
3

Wolfgang Puck 有兩個很特別的習慣：

• 他只做兩種形狀的蛋糕。一種是面積為一單位的方形，另一種是面積為三單位的 L 形。
• 他只用特定尺寸的盒子來裝蛋糕。這些盒子的寛度都是二單位，但各種不同長度都有。

有一天，Wolfgang 想知道有幾種不同的方式可以把蛋糕裝滿一個特定尺寸的盒子。你能幫他嗎？

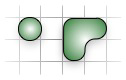
左圖為蛋糕的尺寸，右圖為裝滿長度 6 的盒子的一種方法。

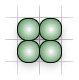
裝滿長度為 2 的盒子的 5 種方法。

Input

輸入的開始有一個 $t$，表示有幾個不同長度的盒子。接下來的 $t$ 行每行有一個整數 $n$ ($1\leq{n}\leq{40}$)

Output

相對於每個 $n$ 輸出一行，該行中的數字為有幾種方法可以用上述的蛋糕裝滿一個 $2\times{n}$ 的盒子。輸出的數字保證小於 $10^{18}$。

Sample Input

2
1
2

Output for the Sample Input

1
5