計算 $R = B^P\mod{M}$

對相當大的 B、P、M 請寫一個有效率的演算法來。

Input

每筆測試資料有 3 行，各有 1 個整數分別代表 B、P、M。

其中 $0\leq{B,P}\leq{2147483647}, 1\leq{M}\leq{46340}$

Output

輸出計算的結果，每筆測試資料一行。

Sample Input

3
18132
17

17
1765
3

2374859
3029382
36123

Sample Output

13
2
13195

經過在百貨公司的一場血拼之後，小梅發現她身上的零錢共有 17 分 (cent，美金貨幣單位，其他貨幣及面值請參考下方紅字部分)，分別是 1 個 dime，1 個 nickel，以及 2 個 penny。隔天，小梅去便利商店買完東西後發現她身上的零錢恰好又是 17 分，這次是 2 個 nickel 及 7 個 penny。小梅就在想，有幾種硬幣的組合可能湊成 17 分呢？經過仔細算算之後，發現共有 6 種。

你的問題就是：給一個金額，請你回答共有多少種硬幣組合的方式。

p.s 美國的零錢共有以下幾種硬幣以及其面值：

• penny, 1 cent
• nickel, 5 cents
• dime, 10 cents
• quarter, 25 cents
• half-dollar, 50 cents

Input

每組測試資料 1 列，有 1 個整數 $n$ ($0\leq{n}\leq{30000}$)，代表零錢的總金額。

Output

對每組測試資料請輸出共有多少種硬幣組合方式。輸出格式為以下 2 種其中之一。

1
2

There are m ways to produce n cents change.
There is only 1 way to produce n cents change.

Sample input

17 
11
4

Sample Output

There are 6 ways to produce 17 cents change. 
There are 4 ways to produce 11 cents change. 
There is only 1 way to produce 4 cents change.

為了呼應台灣電腦彩券的發行，我們特別推出跟組合有關的題目。以台灣的彩券來說，從 46 個球中取出 6 個，共有 C(46,6)=9366819 種組合。(中特獎的機率：1/936681989，夠低了吧！) 給你：

我們可以根據下面的公式算出從 N 個東西中取出 M 個東西的組合數：

你可以假設你的答案 $C$ 不會超出 long int 的範圍。

Input

每筆測試資料一行，有 2 個正整數 $N, M$。$N=0$，$M=0$ 代表輸入結束。

Output

以下列的格式輸出：

N things taken M at a time is C exactly.

請參考 Sample Output。

Sample Input

100  6
 20  5
 18  6
  0  0

Sample Output

100 things taken 6 at a time is 1192052400 exactly.
20 things taken 5 at a time is 15504 exactly.
18 things taken 6 at a time is 18564 exactly.

一個整數 b 如果可以被另一個整數 a 整除 (在這裡 $a > b$)，我們稱 b 是 a 的一個因數。

Perfect Number 是一個正整數並且等於其所有因數的和。例如：6 和 28 都是 perfect number。因為 $6=1+2+3$，$28=1+2+4+7+14$。如果一個正整數不是 perfect，那他就是 deficient 或者是 abundant，根據其所有因數的和是小於或大於這個數本身。因此，9 是 deficient 因為 $1+3<9$。而 12 是 abundant 因為 $1+2+3+4+6>12$。
請寫一個程式求出某一個數是 perfect、deficient 或者 abundant。

Input

有一連串 (不會超過 100 個) 的正整數 n ($1\leq{n} < 60000$)，$n=0$ 代表輸入結束。

Output

請參考 Sample Output。

數字部分佔 5 個字元長度，靠右對齊。與後方的敘述間空 2 個空白格。

Sample Input

15 28 6 56 60000 22 496 0

Sample Output

PERFECTION OUTPUT
   15  DEFICIENT
   28  PERFECT
    6  PERFECT
   56  ABUNDANT
60000  ABUNDANT
   22  DEFICIENT
  496  PERFECT
END OF OUTPUT

Pizza 大家都吃過吧！我個人是偏愛達美樂 Pizza 啦！現在問題來了：給你一塊 Pizza，如果切一刀可以切成 2 塊，切 2 刀最多可切成 4 塊，切 3 刀最多可切成 7 塊 (如下圖)，那切 N 刀最多可以切成幾塊呢？

Input

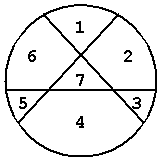
輸入的每一筆測試資料有 1 個整數 N ($0 \leq N \leq 210000000$) 代表切幾刀。

如果 N 為負數，代表輸入結束。

Output

對每一輸入 N，輸出切 N 刀最多可以切成幾塊 Pizza。

Sample Input

5
10
-100

Sample Output

16
56

在統計學的世界中，中間數 (median) 扮演一個重要的角色。 根據定義：中間數就是在一連串已由小到大排序的數字中，排在中間的那一個數。例如：在 {1,3,4,9,11} 中 4 就是中間數。萬一有偶數個數字，我們定義中間數就是位於中間的那 2 個數的和除以 2 (而且只取整數部分)。例如：在 {1,2,3,6,7,8} 中 {3,6} 是位於中間的 2 個數，所以中間數就是 (3+6)/2=4。

Input

輸入包含了 N 個 (N < 10000) 的整數。

Output

對每一個輸入，請輸出到現在為止已輸入的數的中間數。

Sample Input

1
3
4
60
70
50
2

Sample Output

1
2
3
3
4
27
4

據說，90% 的大學一年級新生期望他們自己的成績能在全班平均之上，請你來幫忙驗證看看他們有沒有達成目標。

Input

輸入的第一列有一個整數 $C$ 代表以下有多少組測試資料。每組資料的第一個整數 $N$ 代表班級總人數 ($1\leq{N}\leq{1000}$)。接下來有 $N$ 個以空白或換行來間隔的整數，代表每個學生的期末總成績 ($0\leq{\text{分數}}\leq{100}$)。

Output

對每組測試資料輸出一列，算出有多少百分比的學生成績比全班平均高，請四捨五入到小數第三位。

Sample Input

5
5 50 50 70 80 100
7 100 95 90 80 70 60 50
3 70 90 80
3 70 90 81
9 100 99 98 97 96 95 94 93 91

Sample Output

40.000%
57.143%
33.333%
66.667%
55.556%

某一個粒子有一初速度和等加速度。假設在 $t$ 秒後此粒子的速度為 $v$ ，請問這個粒子在 $2t$ 秒後所經過的距離是多少。

Input

每組測試資料 1 列，有 2 個整數，分別代表 $v$ ($-100\leq{v}\leq{100}$) 和 $t$ ($0\leq{t}\leq{200}$)。

Output

對每組測試資料請輸出這個粒子在 $2t$ 秒後所經過的距離是多少。

Sample Input

0 0
5 12

Sample Output

0
120

你應該有玩過 windows 裡的一個小遊戲叫做 “挖地雷”。這個遊戲的目的就是要在 $M \times N$ 的地雷區格子中找出所有的地雷。為了要幫助你，這個遊戲會在非地雷的格子上有些數字，告訴你這一個格子的鄰居共有多少個地雷。例如：以下 4 * 4 的格子中有 2 個地雷 (以 * 表示)

*...
....
.*..
....

假如我們用上面提到的數字來表現的話可以得到下面的情況：

*100
2210
1*10
1110

可以很簡單的看出，每一個格子最多有 8 個鄰居。

Input

每組測試資料的第一列有 2 個整數 $n,m$ ($0 < n,m \leq 100$)。分別代表地雷區的寬和長。接下來的 n 列，每列有 m 個字元代表地雷區。地雷以 * 表示，非地雷以 . 表示。

當 n=m=0 代表輸入結束。

Output

對每一個地雷區，首先輸出一列：

Field #x:

x 代表這是第幾組測試地雷區。接下來的 n 列表示出以數字取代 . 的地雷區。

測試地雷區之間請空一列。請參考 sample output。

Sample Input

4 4
*...
....
.*..
....
3 5
**...
.....
.*...
0 0

Sample Output

Field #1:
*100
2210
1*10
1110

Field #2:
**100
33200
1*100