一張圖 (graph) $G$ 有一個點集 $V(G)$ 和一個邊集 $E(G)$,其中邊集 $E(G)$ 內的元素是 $V(G)$ 中相異兩個無序點對。
範例一:令 $G$ 是一張圖,$V(G) = \{a, b, c, d\}$ 且 $E(G) = \{(a, b), (b, c), (c, d), (d, b)\}$,下圖給出整個圖 $G$:
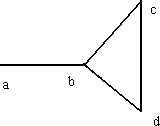
注意圖 G 包含一個「環」$\{(b, c), (c, d), (d, b)\}$。一張缺乏環的圖我們稱為樹 (tree)。圖 G 的一條路徑 (path) 是點和邊的交替序列 (序列是由點開始和結束) 且路徑上所有點皆相異。在範例一的圖中,$\{a, (a, b), b, (b, c), c, (c, d)\}$ 是一條路徑。
事實:樹上任意兩點的路徑是唯一的
如果一張圖任意點對有一條路徑,則圖是連通的 (connected),範例一的圖即是連通的。如果一張圖沒有連通而有數個子圖 (subgraph),則每個子圖被稱為圖 $G$ 的連通分量 (connected component)。
如果一張圖的連通分量都是樹,則整張圖稱為森林 (forest),見下圖。
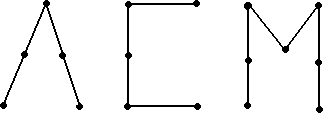
一個值得一提的極端例子,就是若有一個連通分量樹只有一個點而沒有邊,這棵樹就像是一個孤立點,我們稱之為橡實 (acorn)。接下來我們來定義本問題。
問題:給一座森林,請您寫一隻程式計算有幾棵樹和幾個橡實。
Input
輸入檔第一行有一個整數,代表接下來你要處理的測資組數。每組測資包含兩個部分,描述著一座森林:
- 一堆樹的邊 (每個邊佔一行,每行有一對大寫字母,且以一行星號為界)。
- 一堆樹的點 (這些點會在一行,並且最多只會有 26 個大寫字母,對應到 A - Z)
Output
對於每組測試資料,你的程式必須用一句話印出樹和橡實的數量,例如:
「There are x tree(s) and y acorn(s).」x 和 y 分別是樹的數量和橡實的數量。
範例二:令 $G$ 是一張圖,而這張圖是第一筆範例輸入,這張圖就會長得如下圖:
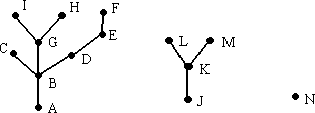
注意:一座森林可能全都是橡實、全都是樹、或者在這之間的所有可能,因此請多注意不要漏掉森林裡的任何一棵樹!
Sample Input
2
(A,B)
(B,C)
(B,D)
(D,E)
(E,F)
(B,G)
(G,H)
(G,I)
(J,K)
(K,L)
(K,M)
****
A,B,C,D,E,F,G,H,I,J,K,L,M,N
(A,B)
(A,C)
(C,F)
**
A,B,C,D,F
Sample Output
There are 2 tree(s) and 1 acorn(s).
There are 1 tree(s) and 1 acorn(s).