許多城市都提供相當完善的公眾交系統,通常會整合公路路線、郊區通勤列車以及地鐵,路線可以根據車站或者是站牌作分類。
為了方便思考,將路線假象成一條線 (從起點發車之後在終點處折返),而循環則是在一條路線中的兩端是相同的。同時可以發現,有些路線非常相似,可以在路線上的幾個站彼此相連,這也是改變路線的唯一方式。
簡化問題後,每一條路線將會由大寫字母 ‘A’ - ‘Z’ 表示,同時每一個路線中將會用小寫字母 ‘a’ - ‘z’ 表示該路線之中的站牌。
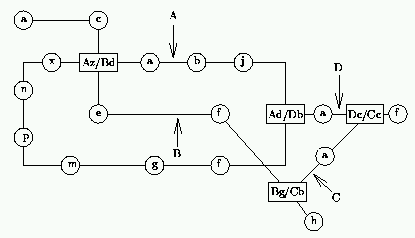
寫一個程式,找到兩站之間的路線使用最少的時間抵達。在同一條路線上移動只消耗 1 單位時間,而在轉運站換搭其他路線消耗 3 單位時間。
Input
輸入分成兩個部分,第一部分描述系統路線,第二部分描述詢問要調查的兩站訊息。
第一部分,一開始會有一個介於 1 到 26 之間的整數 N,表示有多少條路線在系統中,接著會有 N 行,每一行表示一條路線的連接情況。每一行的第一個大寫字符表示路線編號,在 : 之後表示每一站的依序連接方式,如果出現 =,隨後將會出現一個完整的轉運站 (其他路線的站牌) 名稱,有可能會有多個連接情況,如 ...hc=Bg=Cc=Abd...。
如果一條路線呈現環狀,則最後一個站牌編號將會與第一個站牌相同 (只有這種情況才會出現站牌重複地描述)。
接著會有數行詢問,直到遇到 # 終止程式。
Output
對於每組詢問,輸出一行結果。每一行包含所需要的最短時間,輸出寬 3 位向右對齊,隨後接著一個 :,接著輸出最短搭乘路線的順序。保證測資中只會有一條最短時間的搭乘路線。
範例測資如上述給的圖示
Sample Input
4
A:fgmpnxzabjd=Dbf
D:b=Adac=Ccf
B:acd=Azefg=Cbh
C:bac
AgAa
AbBh
BhDf
#
Sample Output
5: Agfdjba
9: Abaz=Bdefgh
10: Bhg=Cbac=Dcf