有句俗話 “不能見樹不見林”,這不僅僅是一句陳詞濫調,而且是錯誤的。真正的問題是你不能見林不見樹。如果你站在樹林(在新西蘭詞彙中是一片灌木的意思)的中間,樹木就會相互遮擋,你能分辨清楚的樹木很少。這種情況在樹木整齊的按行列排布(比如人工松林)時最為突出。本問題是要你來計算當站在人工松林中任意一個點時,你能看清的樹有多少。
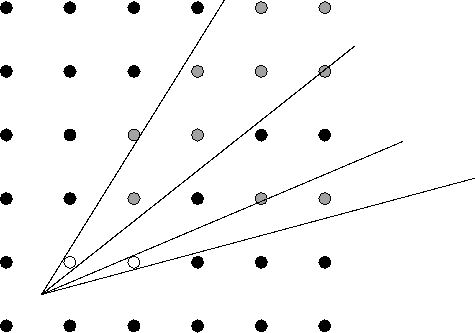
只要當一棵樹的樹幹完全沒有被附近的樹木遮擋時你才能看得清楚——也就是說樹幹的兩側都可以看到,而且兩側離那些更靠近你的樹木之間還有一個可以分辨的間隙。同樣,你不可能看到一棵“太細”的樹。 “不太細”和“可分辨間隙”的嚴格定義是相對你眼睛的視角要大於0.01度(你可以認為是用一隻眼睛來觀查的)。上圖中,按照視角的位置,那兩棵白色的樹至少將所有灰色的樹都擋住了。
給定樹木的直徑,以及眼睛的坐標位置,你寫一個程序計算出在這些條件下能看清多少樹。由於網格無限大,坐標原點就無所謂了,所給的坐標值都介於0到1之間。
Input
輸入由多行組成,每行都包含三個形如0.nn的實數。第一行第一個數為樹幹的直徑——所有樹都認為是一個圓柱體,該值為其直徑,圓柱體的中心都位於坐標網格的交點上,各相距一個單位。後兩個數為觀查者的x和y坐標。為了避免出現潛在的問題,我們保證直徑≤x,y≤(1-直徑)。為避免樹木過小,你可以假定樹木直徑≥0.1。輸入的數據由一行3個0表示結束。
Output
輸出由多行組成,每行輸入對應一行輸出。每行都按給定的樹木尺寸和眼睛位置打印出可見的樹木數量。
Sample input
0.10 0.46 0.38
0 0 0
Sample output
128