給定一圖(V, E),V為節點集合,E為邊的集合,並指定一組有序的節點(V內的所有節點),則一個節點N的bandwidth定義為所有與該節點N相鄰的節點在這一組有序的集合裡面,與該節點N之距離之最大值,而一組有序節點集合O的bandwidth則定義為所有節點的bandwidth之最大值。以下圖為例:
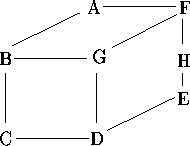
我們隨便把這八個節點作排序,選其中兩組排序如下:
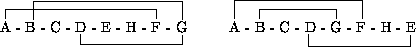
左圖中每個節點的bandwidth由左至右分別為:6, 6, 1, 4, 1, 1, 6, 6,取最大值得到該序列的bandwidth為6,同理,右圖中每個節點的bandwidth由左至右分別為:5, 3, 1, 4, 3, 5, 1, 4,取最大值得到該序列的bandwidth為5。
請寫一個程式,找出一組可能的序列,使得該序列之bandwidth最小。
Input
輸入會有多組測試資料,每組一列表示一組圖形,最後以 # 字元結束輸入。圖形的表示方法是告訴你所有節點與其相鄰的節點,可能的節點名稱為所有大寫英文字母’A’-‘Z’。每組資料以分號 ; 隔開,以測式資料A:FB;B:GC;D:GC;F:AGH;E:HD為例,第一組A:FB表示與A相鄰的節點為F及B,第二組B:GC表示與B相鄰的節點為G及C,以此類推,此例共有5組。
一個圖形最多會有8個節點。
Output
請輸出bandwidth最小的序列,並輸出其bandwidth,格式請參考下面。每個序列中的節點請以一個空白字元隔開,若有多組可能的答案,請輸出字典順序最小的那組。
Sample input
A:FB;B:GC;D:GC;F:AGH;E:HD
A:FB;B:GC;D:GC;F:AGH;E:H
A:B;B:C;C:D;D:E;E:F;F:G;G:H
#
Sample output
A B C F G D H E -> 3
C D B G A F E H -> 2
A B C D E F G H -> 1