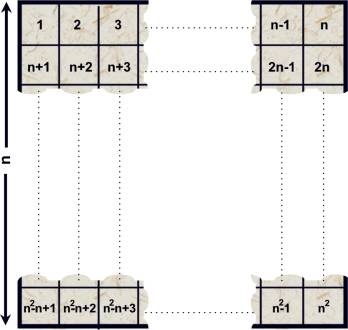
在一個 $n\times{n}$ 的棋盤,王子和公主玩一個遊戲。棋盤的格子以 $1,2,3,\ldots{},n\times{n}$ 來編號,如下圖:
王子從在格子 $1$,跳了 $p$ 步之後抵達格子 n * n。他進入一個格子最多一次。所以如果我們用 $x_i$ 代表他 $i$ 個進入的格子,那 $x_1,x_2,x_3,\ldots{},x_{p+1}$ 都是不同的。請注意 $x_1=1,x_{p+1}=n\times{n}$。公主也做類似的動作,從格子 $1$ 開始,跳了 $q$ 次後抵達格子 n * n。我們用 $y_1,y_2,y_3,\ldots{},y_{q+1}$ 來表示這過程經過的格子。同樣的這 $q+1$ 個數也都不相同。下面圖 2 為一個 3 * 3 的格子矩陣,王子和公主有不同的跳躍路徑。
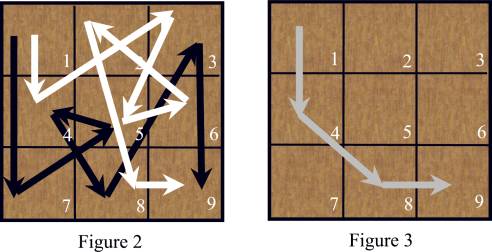
王子的路徑:$1 \rightarrow{7} \rightarrow{5} \rightarrow{4} \rightarrow{8} \rightarrow{3} \rightarrow{9}$ (黑色箭頭)
公主的路徑:$1 \rightarrow{4} \rightarrow{3} \rightarrow{5} \rightarrow{6} \rightarrow{2} \rightarrow{8} \rightarrow{9}$ (白色箭頭)
王子和公主的父親,也就是國王,看到他們玩的遊戲,他說:「為什麼要分開跳?你們是兄妹啊!忽略某些跳躍,使得你們總是在一起。」
假如王子忽略了他的第 2、第 3、第 6 跳,他的路徑變成 $1 \rightarrow{4} \rightarrow{8} \rightarrow{9}$。假如公主忽略了她的第 3、第 4、第 5、第 6 跳,她的路徑變成 $1 \rightarrow{4} \rightarrow{8} \rightarrow{9}$。這共同的路徑 (如圖 3) 就滿足了國王的要求。
國王想要知道王子和公主可以一起移動的最長路徑是多少,你能告訴他嗎?
Input
輸入的第一列有一個整數,代表以下有多筆測資。
每筆測資的第一列有 3 個整數 $n,p,q$ ($2\leq{n}\leq{250},1\leq{p,q}< n\times{n}$),其代表的意義如題目所述。接下來的一列有 $p+1$ 個整數,代表王子的路徑,再接下來的一列有 $q+1$ 個整數,代表公主的路徑。
Output
每組測資輸出這是第幾組測資以及王子和公主最長共同路徑是多長。輸出格式請參考 Sample Output。
Sample Input
1
3 6 7
1 7 5 4 8 3 9
1 4 3 5 6 2 8 9
Sample Output
Case 1: 4