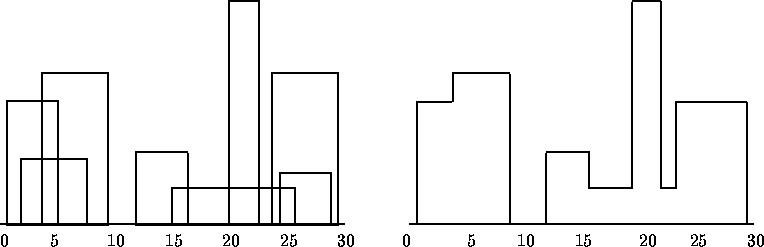
由於高速繪圖電腦工作站的出現,CAD (computer-aided design) 和其他領域 (CAM, VLSI 設計) 都充分使用這些電腦的長處。而在本問題中,你必須幫助建築師,根據他所提供給你都市中建築物的位置,你得幫他找出這些建築物的空中輪廓 (skyline)。為了使問題容易處理一些,所有的建築物都是矩形的,並且都建築在同一個平面上。你可以把這城市看成一個二度平面空間。每一棟建築物都以 $(L_i,H_i,R_i)$ 這樣的序列來表示。其中 $L_i$ 和 $R_i$ 分別是該建築物左邊和右邊的位置,$H_i$ 則是建築物的高度。下方左圖就是 $(1,11,5)$、$(2,6,7)$、$(3,13,9)$、$(12,7,16)$、$(14,3,25)$、$(19,18,22)$、$(23,13,29)$、$(24,4,28)$ 這八棟建築物的位置圖。而你的任務就是畫出這些建築物所構成的輪廓,並且以 $(1, 11, 3, 13, 9, 0, 12, 7, 16, 3, 19, 18, 22, 3, 23, 13, 29, 0)$ 這樣的序列來表示如下方右圖的輪廓。
Input
只有一組測試資料。
每列有一棟建築物的資料。建築物不會超過 $5000$ 棟。所有的數字都小於 $10000$。並且建築物已按照 $L_i$ 排好序。
Output
輸出為描述建築物輪廓的向量。在輪廓向量 $(v_1,v_2,v_3,\cdots{},v_{n-1},v_n)$ 中,在 $i$ 為奇數的情形下,$v_i$ 表示一條垂直線 ($x$ 座標),在 $i$ 為偶數的情形下,$v_i$ 表示一條水平線 (高度)。輪廓向量就像一隻蟲從最左邊建築物走起,沿著輪廓路徑水平及垂直的行走的路徑。所以最後輪廓向量的最後一個數一定為 $0$。
請參考Sample Output。
Sample Input
1 11 5
2 6 7
3 13 9
12 7 16
14 3 25
19 18 22
23 13 29
24 4 28
Sample Output
1 11 3 13 9 0 12 7 16 3 19 18 22 3 23 13 29 0