Background

Filters(一種程式，用於資料過濾並重新格式化輸出)是UNIX系統上的一個重要的程式類別，而管線(pipe)是作業系統裡的一個概念，能讓資料在行程(processe)間流通(並使多個filter能輕易地串在一起)。

本題討論如何使裝進容器內的管線(pipe)數量最大化，但這並非是一個裝箱問題 (bin packing problem)，而是一個 pipe fitting problem。

有一群會互相贈送禮物的朋友，每次收到與送出禮物的價值皆不同，本題要來計算每個人損益情形。

本題中每人都設定一筆買禮物的預算，預算會平均分配買等值的禮物送給他的朋友們。

然而，任何小團體中總有一些人比較慷慨(或是與其他的的關係比較好)，也總有一些人比較有錢。

給你一群朋友的資料，包含每人買禮物的預算，及禮物會送給那些朋友。你必須寫一個程式來計算每個人的損益情形。

由於紐西蘭今年冬天發生能源危機 (因為久旱不雨，導致水庫水位太低)，所以必須實施一個非常態性的限電措施，就是讓每個地區公平地輪流斷電一段時間。全國被分成 N 個區域 (Auckland 編號為 1, 而 Wellington 編號為 13)，先隨機選定一個整數 m，再從編號為 1 的地區開始限電，以此之後的第 m 個地區為下一個斷電的地方，若計算到最後一個編號則從頭開始循環，並拒除已經斷過電的地區，例如當 $N=17, m=5$，則各地區停電的順序為 1, 6, 11, 16, 5, 12, 2, 9, 17, 10, 4, 15, 14, 3, 8, 13, 7。

本問題要求最後一個斷電的地區為編號 13 的 Wellington 地區 (因為那是電場總部的所在地)，所以對於不同的 N 值必須小心地選擇 m 值使得編號 13 為最後停電的地區。

請寫出一個程式讀取 N 值，並計算達成條件要求的最小 m 值為何。

Background

圖論是計算機科學的一個重要分支，至少可追朔到十八世紀尤拉(Euler)所解決著名的七橋問題(Seven Bridges of Königsberg)，許多最佳化問題都涉及到如何有效處理圖形問題。

本問題要求計算郵差徒步送信的最短路徑。

The Problem

給定數條街道的資訊(以十字路口連接不同道路)，你的程式必須計算走過全部的街道所需的最短距離，路徑的起點與終點必須一致。

你可以想像在現實世界中有一位郵差，他先把車開到十字路口之後再走路到各個巷弄把附近需要遞送的郵件一一送完，之後再走到車子所在的路口開往下個地點送信。

行經一條街道的距離直接等於街道的長度(不管該道路有沒有信要送，都必須走完整條道路的距離)。

本問題中，在路口交會的所有道路數目被稱做該路口的”層級”(degree)，最多只會有兩個路口的”層級”為奇數，其他所有路口皆為偶數，也就是只會有偶數條道路在此路口交會。

Loglan 是一種綜合型可發音的語言，設計它是用來驗證語言學上的一些原則性問題，比如薩皮爾—沃爾夫假說。它的句法精確明了，在文化上趨於中立，它的哲學是能省則省。該語言的語法集已經被過份的簡化——只有 200 條語法規則。

Loglan 的語句由一系列的單詞和名稱組成，中間由空格隔開，並由一個點號（.）表示結束。

Loglan 的單詞均以元音結束；名稱來自於該語言之外，由輔音結束。 Loglan 的單詞分為兩類——小單詞和謂詞。小單詞指定了句子的結構；謂詞的形式為“CCVCV”或“CVCCV”，其中C代表一個輔音，V代表一個元音。 （見下面的例子）

我們考慮使用 Loglan 語言的一個子集，具有以下語法定義：

A → a | e | i | o | u
MOD → ga | ge | gi | go | gu
BA → ba | be | bi | bo | bu
DA → da | de | di | do | du
LA → la | le | li | lo | lu
NAM → {all names}
PREDA → {all predicates}
<sentence> → <statement> | <predclaim>
<predclaim> → <predname> BA <preds> | DA <preds>
<preds> → <predstring> | <preds> A <predstring>
<predname> → LA <predstring> | NAM
<predstring> → PREDA | <predstring> PREDA
<statement> → <predname> <verbpred> <predname> | <predname> <verbpred>
<verbpred> → MOD <predstring>

(譯註：上面文法中NAM為所有名稱的符號，PREDA為所有謂詞的符號）

寫一個程序，讀入一組字符串並確定它們是不是正確的Loglan語句。

在公元前45年，凱撒大帝頒布了標準曆法——每年有365天，每4年閏一天，閏在2月的29日。然而此曆法並不能精確的表示一個太陽年，季節開始地越來越早引起了人們的注意。到1582年，教皇格利戈里八世規定了新的曆法，從那以後，所有能被100整除的年份中只有能被400整除的才是閏年。另外，當年的日曆要按照新曆法進行調整才能與季節吻合，1582年10月4日（週四）的後一天定為1582年10月15日（週五）。新曆法和調整方案被羅馬天​​主教國家迅速採用，但英國和美國（還包括其它一些國家）直到1752年才開始採用，是年9月2日（週三）的後一天定為9月14日（週四）。 （俄國直到1918才作出調整，而希臘則維持舊曆直到1923年）因此有很長一段時期的歷史是以兩種不同的紀年方式記載的。

寫一個程序，讀入日期並確定是哪一種曆法，然後將該日期轉換到另一種曆法。

想像一個n行n列的網格，我們要在每行每列都標註k個交點，使得這些交點中的任意4個所構成的矩形（如果可以構成矩形），都不存在與網格線平行的邊。比如 k = 2 和 n = 3 的情況，可能的解如下：

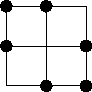
易知，對於任意的 k，n 的最小值為：$k^{2}-k+1$。更進一步來講，n 也不會比這個值更大。

寫一個程序，計算所有 k ≤ 32 的解。 k-1 可能是0，1 或任何素數。

觀察上圖中的三個物體。它們均由多邊形表示，並給定其重心和各頂點的坐標。在上圖中，重心由黑色方塊表示。頂點的編號按逆時針方向依次給出。

將一個物體的輪廓多邊形上某兩個頂點連成一條線段，且該線段未穿越多邊形的內部，然後通過旋轉多邊形使該線段達到水平，若重心在這條線段之上且位於線段兩端點之間，就認為該物體可以擺放平穩。一般情況下，物體有多個可以放穩的位置，每個穩定位置均由對應的線段（稱作“基線”）表示。一條基線會經過至少兩個多邊形上的點（即端點），基線就由這些點中最大的編號表示。

寫一個程序計算出編號最小的基線。對於上圖中的物體，“object 1”要求的基線為 6，“object 2”為6，“square”為 2。你可以假設物體都是規則的，即不存在自相交的輪廓多邊形，但有可能是凹多邊形。

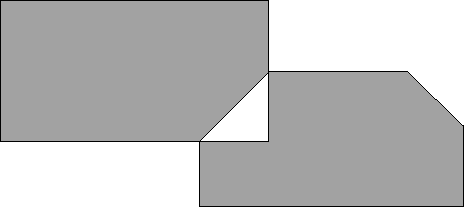
給定兩個可能相互重疊的凸多邊形。如果存在重疊，其重疊的角度和方向各異。你要寫一個程序讀入兩個凸多邊形各角點的坐標，併計算出二者“異或”得到的區域的面積，也就是在二者全部區域中僅存在其中一個多邊形的區域。要求的面積如下圖所示：