本題請你做四則運算,計算某數 n 乘上 567 後除以 9,再加上 7492,再乘上 235,再除以 47,最後減掉 498,請問其值的十位數值是多少?
Input
第一列的整數 t 表示測試資料的組數,每組測試資料有一個整數 n ($-1000\leq{n}\leq{1000}$),一筆資料一列。
Output
請依要求輸出每筆資料的結果。
Sample Input
2
637
-120
Sample Output
1
3
本題請你做四則運算,計算某數 n 乘上 567 後除以 9,再加上 7492,再乘上 235,再除以 47,最後減掉 498,請問其值的十位數值是多少?
第一列的整數 t 表示測試資料的組數,每組測試資料有一個整數 n ($-1000\leq{n}\leq{1000}$),一筆資料一列。
請依要求輸出每筆資料的結果。
2
637
-120
1
3
Extel 推出最新型的電腦「X9091 字串處理機」,主要用途在於密碼學上的應用。該電腦可藉由編程由一組輸入字串產生另一組字串,該電腦用的是精簡指令集晶片 (RSIC),只有三個指令:
D) 特定位置上的字元。I) 一個字元到特定位置。C) 特定位置上的字元。電腦程式是由機器語言所寫成,且每個指令為固定長度,格式為 ZXdd,Z 表示刪除 (D)、插入 (i)、改變(C) 其中之一,X 表示字元,dd 表示兩位數字。程式的結束以一個特殊的結束指令 E 來表示。
以一個例子來說明,若輸入字串為 abcde,我們希望藉由字串的運算得到 bcgfe,以下是一個比較簡單的運算方式:
| 指令 | 字串 | 備註 |
|---|---|---|
abcde |
||
Da01 |
bcde |
% a 是必要的 |
Cg03 |
bcge |
|
If04 |
bcgfe |
|
E |
bcgef |
% 程式結束 |
寫一個程式讀入兩組字串 (輸入字串與目標字串),並找到由輸入字串轉換成目標字串最少所需的指令總數,若有多種可能的解法,只要輸出任一種就可以了。
輸入有許多列,每列有兩個字串,並以一個空白字元分隔。字串長度不會超過 20 個小寫字元,以 # 表示輸入結束。
abcde bcgfe
#
Da01Cg03If04E
威廉博士是一位著名的植物心理學家,他發明了一種新的植物分類法,這是個複雜的分類法,在分類之前必須先對每顆樹定義三個一組的參數(每個參數值在[0, 255]的範圍),因此每顆樹可被視為三維空間內的一點。基於自然的生長法則,測量大樣本數量的樹木通常都會均勻地分佈在整個空間。博士發現在空間內相鄰的樹木之間有很高的相似性,為了要驗證這項假設,他必須統計每顆樹與其最靠近的樹木的距離,並依固定的距離組距做成直方圖。
請寫一個程式最多可處理5000顆樹,並決定每一顆樹與其最接近的樹的距離小於1的共有幾顆,大於等於1且小於2的有幾顆,以此類推,直到統計出大於等於9且小於10的有幾顆。因此,假如 di 定義為第 i 顆樹與其最靠近的樹的距離,且 j<= di < k (其中 k = j+1),則這顆樹就在直方圖 j 的那一組的數量加1(最小一組為第0組)。例如,若共有兩顆距離為1.414單位的樹,則直方圖每組的長度為:0, 2, 0, 0, 0, 0, 0, 0, 0, 0。
放石頭遊戲(The game of Spot)在一塊 NxN 的板子上進行,如下圖為N=4的板子。遊戲的玩法是兩個玩家輪流放一塊石頭在空的格子上,或是可以從板子上拿一塊石頭起來,遊戲的進行中可以發現,板子上 石頭的佈局會不斷變化,當一玩家排出已重複出現過的佈局時,他就算輸了這一局(一種佈局如果將之旋轉90度、180度、270度亦視為相同的佈局)。若在 2N步內未出現過相同的佈局就算和局。
請參考下列幾種佈局:

若 出現過第一種佈局,則再出現2、3、4種佈局即結束比賽(還有另一種能結束比賽的佈局未畫出),注意,第5種佈局並不能算是相同的佈局。
某國政府為了降低申請助學貸款的意願,設計了一套費時而又冗長的請款流程,每位申請的學生會收到一張提款卡,記錄目前已提領的金額,一開始已提領金額當然為零,且每年的提領上限為 $\$ 40$。詭異的是,領款時間只限該學生生日後的第一個銀行工作日,所以通常一天最多只有 25 個學生會來領錢。
學生必須拿著提款卡到特定的提款機領錢,這種提款機被設計成有極佳的安全性,它有兩層金庫,安全性較高的內層金庫有許多 $\$1$ 元硬幣,而安全性較低的外層金庫則負責儲放少量的 $\$1$ 元硬幣供學生直接提領。為了降低被搶所造成的損失,只有當外層金庫的硬幣用完的時候,才會由系統自動把硬幣由內層移到外層。每天一開始外層金庫會是空的,且馬上會有 $\$1$ 元硬幣由內層移往外層,之後當外層金庫的硬幣被領完的時候,由內層移往外層的硬幣會增加到 $\$2$,下次再領完則再增加到 $\$3$ … 以此類推,直到到達某一個最大值 k 為止,下次移往外層的金額又會由 $\$1$ 開始累加。
每位學生排隊領 $\$40$,領錢時會插入自已的提款卡,提款卡會記錄已提領的總金額。每次領錢最多只能領到外層金庫內的硬幣金額,若學生總提領金額未到達 $\$$40,則他會拿回他的提款卡到後面重新排隊,當然,此時外庫金庫的金額為零,系統會馬上補上一筆錢到外層金庫。若外層金庫的金額加學生已提領總額大於 $\$$40,則系統只會發出剛好總額達到 $\$$40 的錢給學生,剩下在外層金庫的錢會留下來給下一位學生提領。
請寫程式處理兩個整數為一組的資料,N表示學生數($1 \le N \le 25$),k表示提款機硬幣由內移往外層的最大限制($1 \le k \le 40$),請依序輸出學生領滿 $\$40$ 後離開的次序。
由輸入資料產生出肯定或否定(yes or no)兩種答案的問題被稱為「判定性問題」(decision problems)。一個典型的判定性問題是NP-完備性問題(NP-complete problems),這種問題並無法用一般通用而有效率的方法處理。有些問題與判定性問題一樣單純,不過要試著列舉出所有肯定的答案就很困難了(或至少會花很多時間)。
這問題關於車輛在一個僅含單向道路的城市中,如何決定所有可能路徑的總數。
給定城市中所有由道路連接的交叉點,你必須寫一個程式決定每個交叉點之間所有可能路徑的總數,一條路徑是由一節點到另一節點之間所依序經過的道路集合。
城市內的點由 0 開始被賦予編號,一條單向道路會由兩個節點來指定,例如 $ j \; k $ 表示由節點 j 到節點 k 的單向道路,注意,雙向道路可藉由定義兩條對向的道路來處理:$ j \; k $ 與 $ k \; j $ 。
考慮一個有四個節點,並以以下四條單向道路所連結的城市:
0 1
0 2
1 2
2 3
由 0 到 1 之間共有 1 條可能的路徑,由 0 到 2 之間共有 2 條可能的路徑($0\rightarrow 1\rightarrow 2$ 及 $0 \rightarrow 2$ ),由 0 到 3 有 2 條路徑,1 到 2 有 1 條,1到 3 有 1 條,2 到 3 有 1 條。
兩點之間的路徑可能存在有無限多條,例如上例中再增加一條由 3 到 2 的路徑,則由 0 到 2 的路徑選擇會變的有無限多條,因為可藉由 2 3 之間來來回回來增加路徑總數,因此路徑 $0\rightarrow 2\rightarrow 3\rightarrow 2\rightarrow 3\rightarrow 2$ 與路徑 $0\rightarrow 2\rightarrow 3\rightarrow 2$ 是不同的。
給定一圖(V, E),V為節點集合,E為邊的集合,並指定一組有序的節點(V內的所有節點),則一個節點N的bandwidth定義為所有與該節點N相鄰的節點在這一組有序的集合裡面,與該節點N之距離之最大值,而一組有序節點集合O的bandwidth則定義為所有節點的bandwidth之最大值。以下圖為例:
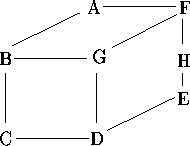
我們隨便把這八個節點作排序,選其中兩組排序如下:
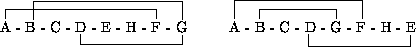
左圖中每個節點的bandwidth由左至右分別為:6, 6, 1, 4, 1, 1, 6, 6,取最大值得到該序列的bandwidth為6,同理,右圖中每個節點的bandwidth由左至右分別為:5, 3, 1, 4, 3, 5, 1, 4,取最大值得到該序列的bandwidth為5。
請寫一個程式,找出一組可能的序列,使得該序列之bandwidth最小。
給你一組標題字串,並告訴你那些是相對不重要的字,請你寫一個程式找出標題字串中所有關鍵字(Key Word In Context),並依照關鍵字的字典順序依序列出。
關鍵字是除了所有不重要的字以外的字,而我們會給你那些不重要的字。
例如,不重要的字若為:``the, of, and, as, a’’,且有四組標題列:
Descent of Man
The Ascent of Man
The Old Man and The Sea
A Portrait of The Artist As a Young Man
而我們需要你依字典順序找出所有關鍵字後,把整個標題列出,並把關鍵字改為大寫:
a portrait of the ARTIST as a young man
the ASCENT of man
DESCENT of man
descent of MAN
the ascent of MAN
the old MAN and the sea
a portrait of the artist as a young MAN
the OLD man and the sea
a PORTRAIT of the artist as a young man
the old man and the SEA
a portrait of the artist as a YOUNG man
國防部的軍事武器承包商剛完成一種新式飛彈防禦系統的測試工作,該系統稱為 CATCHER,可以攔截朝我方發射過來的飛彈,該系統非常強大,有極佳的機動性及自我防禦能力,但它有一個缺點:雖然它能攔截的飛彈高度沒有上限,但是能攔截的飛彈高度只能比上一次攔截的高度更低或相等,它沒有足夠的動力攔截更高的飛彈。
承包商所做的電腦模擬測試相當簡單,僅僅只做高度測試,也就是每隔一段時間就會有一顆欲攔截的飛彈,並顯示該飛彈可以被攔截到的高度,所有飛彈都是循序的。
測試報告中只會循序顯示所模擬的飛彈高度,及所有這些飛彈中可以被 CATCHER 攔截到的總數。
現在國防部需要驗證承包商所做的測試報告的正確性,你必須幫忙寫一個程式循序讀入多組飛彈高度,並計算 CATCHER 系統最多可攔截的飛彈總數,請注意到 CATCHER 系統本身的限制,當他選擇攔截某一顆飛彈之後,再也不能攔截更高的飛彈了。
輸入包含多組測試資料,每組資料會有多非負整數,其值介於 0 ~ 32767 之間,用來表示飛彈的高度,測試資料的最後以 -1 表示該組資料結束,並非表示飛彈的高度。如果該組測試資料的第一個數值為 -1,表示測試資料結束。
請輸出每組測試資料的編號 (Test #1、Test #2、…),及在該組資料下 CATCHER 系統所能攔截到的最大飛彈總數,輸出的格式如下所示。並請注意每組輸出資料之間請以空行隔開。
注意:每組測試資料的飛彈總數並沒有限制,所以一個效率不佳的演算法可能無法在時限內完成問題。
389
207
155
300
299
170
158
65
-1
23
34
21
-1
-1
Test #1:
maximum possible interceptions: 6
Test #2:
maximum possible interceptions: 2
如果我們要用常見的長度為高度兩倍的磚塊建一道磚牆,並且牆的高度為兩個單位,根據牆的長度,我們可以建出不同數量的花樣。從圖一我們可以看出:
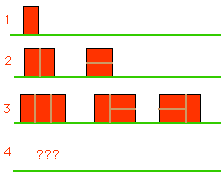
長度為 4 的牆你可以找出幾種花樣?那長度為 5 的牆呢?
你必須寫一個程式計算當牆的長度給定之後,決定共有多少種排列方式。
你的程式會從輸入中讀取一連串的正整數,每個正整數一列表示牆的長度,最大值為 50,並以 0 表示輸入結束。
對應輸入中每列牆的長度,請輸出共有幾種排列方式。
1
2
3
0
1
2
3