給你一個由字元構成的矩形以及座標 $(r, c)$,請求出由相同字元所構成的最大正方形。$(r, c)$ 代表此最大正方形的中心,矩形的左上角座標為 $(0, 0)$,右下角為 $(M-1, N-1)$。以下圖來說,給你座標 $(1, 2)$,則此最大正方形的邊長為 3。
abbbaaaaaa
abbbaaaaaa
abbbaaaaaa
aaaaaaaaaa
aaaaaaaaaa
aaccaaaaaa
aaccaaaaaa
給你一個由字元構成的矩形以及座標 $(r, c)$,請求出由相同字元所構成的最大正方形。$(r, c)$ 代表此最大正方形的中心,矩形的左上角座標為 $(0, 0)$,右下角為 $(M-1, N-1)$。以下圖來說,給你座標 $(1, 2)$,則此最大正方形的邊長為 3。
abbbaaaaaa
abbbaaaaaa
abbbaaaaaa
aaaaaaaaaa
aaaaaaaaaa
aaccaaaaaa
aaccaaaaaa
對於一個 N 維 ($1 < N < 15$) 的單位正方體中,每個角落都有他的重量 (小於 256)。如果兩個角落有相同的邊,我們稱這兩個角相鄰 (neighbouring)。一個角落的效力 (Potency) 是其所有相鄰角之和。現在給你所有角落的重量,請求出二個相鄰角效力和的最大值。
Hasan 和 Tanveer 在班上是對調皮的小孩,只要一有機會坐在後面的座位,他們上課時間就會玩井字遊戲 (Tic Tac Toe)。但他們老師不認為上課玩圈圈叉叉是件好玩的事,所以某天老師看到他們在玩遊戲,就把他們抓到前面的座位聽課。
但想也知道,上課是件很無聊的事,所以沒過多久 Hasan 和 Tanveer 就睡著了,老師看到了,就把他們叫去解決又臭又長的題目。解題的過程中,他們極盡所能不讓老師抓到他們玩遊戲,但悲慘的是--他們又被抓包了! (可憐的 Hasan 和 Tanveer,難道老師一點也沒有同情心嗎?)
這次老師很生氣所以丟給他們一道超困難的問題,這道題目是這樣的:將 1 到 1000 依序串接寫成一個一千位數的數字。可憐的兩人只好安分的做這項作業。
這時班上兩位同學 Alam 和 Dalim 開始思考:如果依序寫下所有數字的話,那麼這個數字應該會長得像 1234567891011121314 … 這個樣子,但這項工作非常耗時,因此,他們會因為數錯位數而答錯答案,因此他們想要找一個方法把老師的答案騙過來。你能幫助他們嗎?
高中物理老師通常認為問題當中的文字敘述比純計算還要難,畢竟,身為學生必須得先讀懂題目才行!
所以老師們不會把題目寫成這樣:「電壓為 10 伏特、電流 5 安培、求電功率?」 ($U=10V$, $I=5A$, $P=?$) 而是喜歡把題目弄這樣:「你有一組電路,電路裡包含了一顆 10 伏特的電池和一枚燈泡,若現在有一 5 安培的電流通過此燈泡,那麼燈泡的電功率為何?」 (You have an electrical circuit that contains a battery with a voltage of $U=10V$ and a light-bulb. There’s an electrical current of $I=5A$ through the bulb. Which power is generated in the bulb?)
然而,半數的學生不會去鳥題目到底寫了什麼,只會設法從題目中找出已知條件:電壓 10 伏特、電流 5 安培,然後思考:「我該用什麼公式?噢,對了!$P = I\times{V}$,因此我可以得到電功率為 $10 \times{5} = 500$ 瓦特,完成。」
沒錯,但這個方法並不是每次都有用,所以這些學生在物理考試都考不高,但至少可以寫一個間單的程式來讓班上的人通過考試。 (雖然很遺憾但這是事實)
現今我們將測試電腦是否可以通過高中物理考試,我們先解決電功率–電壓–電流類型 (P-U-I type) 的題目。這意味著給你兩個已知的條件,然後求出第三項的值。
你的工作就是寫一支程式讀入一段題目,然後用簡單的演算法解出答案。
Soundex 編碼系統 (Soundex coding) 是依據字母的拼音來編碼,舉例來說,「can」和「khawn」、「con」和「gone」會因為讀音相近而在 Soundex 編碼下有相同的值。
數學界中,黎曼假設 (Riemann Hypothesis)被數學家們稱之為最大為解決的難題之一:「對於所有黎曼 ζ 函數 (zeta function) 中非平凡零點 (non-trivial zeros) 的實數部分是二分之一。」那麼現在給你一個很簡單的題目:對於每個正整數 N,請輸出第 N 個零點 … 呵,開玩笑的!這樣子這道題目會變得太複雜,我們可以選擇計算比較簡單而且跟黎曼函數相關的梅登函數 (Mertens’s function)。如果有興趣想要知道的話,請參閱 Derbyshire 的書 (見後記)。
對於每個大於 1 的正整數,我們可以把它質因數分解。有些數字像 2、7、11 等只有一個因數的數,我們稱它為質數 (prime numbers)。其他數字像 4 (2×2)、15 (3×5)、144 (2^4×3^2) 我們稱它為合數 (composite numbers)。如果一個數的每個質因數都只有一個,我們稱它為 square free,有些合數像 21 (3×7)、187 (11×17) 就是 square free,而有些合數像 9 (3^2)、98 (2×7^2) 則不是。
於是我們先定義默比烏斯函數 (Möbius function) 為 mu(N),對於每個正整數 N:
接著,我們可以定義梅登函數 (Mertens’s function) M(N)為默比烏斯函數從 1 到 N 的級數和:
M(N) = mu(1) + mu(2) + … + mu(N)。
下列為前 20 個默比烏斯函數及梅登函數的值:
| N | 質因數 | mu(N) | M(N) |
|---|---|---|---|
| 1 | - | 1 | 1 |
| 2 | 2 | -1 | 0 |
| 3 | 3 | -1 | -1 |
| 4 | 2 2 | 0 | -1 |
| 5 | 5 | -1 | -2 |
| 6 | 2 3 | 1 | -1 |
| 7 | 7 | -1 | -2 |
| 8 | 2 2 2 | 0 | -2 |
| 9 | 3 3 | 0 | -2 |
| 10 | 2 5 | 1 | -1 |
| 11 | 11 | -1 | -2 |
| 12 | 2 2 3 | 0 | -2 |
| 13 | 13 | -1 | -3 |
| 14 | 2 7 | 1 | -2 |
| 15 | 3 5 | 1 | -1 |
| 16 | 2 2 2 2 | 0 | -1 |
| 17 | 17 | -1 | -2 |
| 18 | 2 3 3 | 0 | -2 |
| 19 | 19 | -1 | -3 |
| 20 | 2 2 5 | 0 | -3 |
請求出對於一正整數 N 的 mu(N) 和 M(N)。
編碼 (encoding) 技術通常用在需要加密或者是節省儲存或傳輸空間的時候。所以現在,我們使用較簡單的編碼技術,來將不多於五個字母的合法字做編碼。
所謂的合法 (valid) 字,是說一個合法字裡面,下一個字元一定比上一個來的大,例如:abc、aep、gwz 為合法字,而 aab、are、cat 為不合法的。
現在我們將合法字依字典順序編碼如下:
a -> 1
b -> 2
.
.
z -> 26
ab -> 27
ac -> 28
.
.
az -> 51
bc -> 52
.
.
vwxyz -> 83681
你的任務就是要讀入一個字,然後輸出它的編號。如果該字不合法,請輸出 0。
寫一支程式把羅馬數字轉換成十進位的阿拉伯數字。
以下是羅馬數字代表的代號:$I=1$、$V=5$、$X=10$、$L=50$、$C=100$、$D=500$、$M=1000$,此外還有一些兩個字合體的代號:$IV=4$、$IX=9$、$XL=40$、$XC=90$、$CD=400$、$CM=900$。
請記得,這支程式必須排除不合理的羅馬數字。
你喜歡薩克斯風嗎?我有一個降 E 中音薩克斯風 (Eb Alto Saxophone),如下圖 (圖略)。
當我在演奏某些手指必須動很快的曲子時,我忽然想到:到底我的手指頭按了幾下按鍵?假設每首曲子由某一個八度的 C、D、E、F、G、A、B 和高一個八度的 C、D、E、F、G、A、B 的音調 (note) 所組成,我們使用 c、d、e、f、g、a、b、C、D、E、F、G、A、B 來代表他們。每個音調的指法如下:
(假設每種不同的指法控制一種音調,而且一個手指頭按特定一個按鍵)
所以請寫出一支程式去計算每一根手指頭按了多少次按鍵。如果某一按鍵在下一音符時不會用到,那麼就會放開,否則就是維持按著的情況。
露西 (Lucy) 和莉莉 (Lily) 是雙胞胎,而今天是她們的生日,媽媽買了一個生日蛋糕給她們。現在我們把蛋糕放在平面座標上,蛋糕中心的座標為 (0, 0),而蛋糕的半徑為 100。
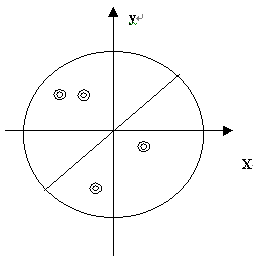
蛋糕上面有 2N ($1\leq{N}\leq{50}$) 個櫻桃,媽媽想把蛋糕切成兩半 (當然是直線),可是雙胞胎希望能夠把蛋糕平分而且兩塊蛋糕上有一樣多的櫻桃 (這意味著這條直線要切過中心),你可以幫她嗎?
注意:櫻桃的座標 (x, y) 為兩個整數,所以你必須找到兩個整數 A, B 使得 $Ax + By = 0$,A 和 B 的範圍介於 -500 到 500 間,櫻桃不能位在線上。對於每個測資至少有一組解。