在幾何學上，一個超立方體 (hypercube) 為一個類似正方形 (2 維) 或者是正方體 (3 維) 的 n 維物體。它由許多群互相平行且等長的線段所組成，群與群之間彼此互相垂直排列著，一個 n 維的超立方體也稱為 n 次方體 (n-cube)。
在平行運算 (parallel computing) 中，頂點代表處理器，而線段 (邊) 代表連接網絡，一個 n 次方體結構有下列特性：
每個節點與其他 n 個不同的處理器相聯接。
每個處理器擁有唯一的識別碼，識別碼介於 $0$ 至 $2^n-1$。
若兩個處理器的識別碼只有一位元的差異，則此二處理器為直接相連。舉例來說，處理器 3 (二進位表示為 011) 和處理器 7 (111) 為直接相連。
處理器的數量為 $2^n$ 個。
新成立的公司 WELAIL 正設計超立方體，但他們總是與一些不知道超立方體特性的人簽約，因此他們時常製作失敗，也就是說每一次的專案中的產品不一定滿足上述的特性。給你任意一張圖，你的任務就是去寫一個程式來確定是否為超立方體。
Bididibus 是一個古老的二維世界，Bididibus 人居住在此。Bididibus 人擁有他們的 2D 山、2D 水、1D 電視，甚至還有令人驚奇的最新科技──2D 電影！最近，Bididibus 的學者向大眾警告全球暴雨 (global raining) 的危險性，這個氣候災難將會把全世界的溪谷都注滿了水。
Bididibus 擁有一樣高及一樣寬的單位地形。在 Bididibus 山海經 (Bididibusian orography) 一書中，使用一系列的符號，從左至右描繪出單位地形的起伏 (書中使用「/」代表地形攀升、「\」代表地勢下滑、「_」代表地形平坦)。
舉例來說，我們可以有像下圖的 2D 世界：
_
/ \
/ \__/\_
/\_ _/ \ _
/\/ \_/ \_/ \ /\
/ \/\/
顯然地，當地的地理學家都是 ASCII 藝術的狂熱者，他們使用一種更為簡化的表示方法：將所有的地形起伏寫在一行中。則先前該 2D 世界則表示為：
//\//\_\_/_///_\\__/\_\\_/_\\/\//\
在全球暴雨後，大水將會填滿所有溝渠，如果我們用藍色代表淹水區域，我們會得到下圖的結果：
由觀察而得，在含有「/」或「\」的方格中，洪水只填滿 1/2 單位的體積，而在全為藍色的方格中，大水則填滿 1 單位的體積。舉例來說，在先前的 2D 世界中將會被填滿 21 單位體積的水。
現在給你一個以簡化符號所代表的世界，你的任務就是計算出在全球暴雨後所覆蓋的水體積。
西元前 3000 年，埃及人已有了象形文字做為書寫系統，而在數字表示上，埃及人使用 10 進位並以各種象形文字來表示，如圖，他們使用一根長棍代表一、倒轉 U 當作十、螺旋當作百、似紙的植物當作千、手指當做萬、蝌蚪當作十萬以及一個跪著的人當作一百萬。
舉例來說，如果要書寫出 276 這個數字，則需要十五個象形文字：兩個「百」、七個「十」和六個「一」的圖形。則 276 的表示法如下：
則數字 4622 將會以這樣子表示：
就如你所見，埃及人根據符號的大小，依序從左至右或者從右至左書寫。
你必須將象形文字所表示的數字轉為阿拉伯數字，而我們可利用下表將象形符號使用英文字母代表：
因此，我們可以將 276 表示為 SSUUUUUUUBBBBBB 或是 BBBBBBUUUUUUUSS，但每個符號不能書寫超過九次。
John Anthony Good 常常與他的好友在星期五的晚上通霄打牌，他們玩的是現今最熱門的撲克牌遊戲 Texas Hold’em，在 Texas Hold’em 的遊戲中，每位玩家運用 2 張蓋著的牌來跟 5 張攤開的牌做組合，以組成一副最大的 5 張牌牌組，當然玩家們可以用蓋牌的兩張、其中一張或是都不用來組成。
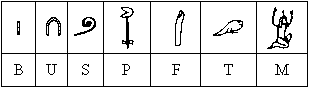
一副撲克牌有 52 張牌，由四樣花色 (黑桃、紅心、磚塊和棉花) 以及每樣花色 13 支牌 (由小到大依序為 2、3、4、5、6、7、8、9、T、J、Q、K 和 A) 所組成。玩家可出的牌型只能依照下面其中一種：
同花順 (Straight Flush) ：五張牌數字連續並且相同花色。例：6H、7H、8H、9H、TH。注意 A 可以當作最小的牌接在 2 之後，例如：AS、2S、3S、4S、5S。如果出現兩個以上的同花順，則比較牌組中最大的牌，上述兩例中前者大於後者。
鐵支 (Four of a Kind) ：其中四支牌為相同數字。例：AS、AD、AH、AC、3S。如有兩者以上則比較四支牌的數字大小，然而為了避免打平的情況發生，則再需比較餘下一張牌的大小。
葫蘆 (Full House) ：其中三張牌為相同數字，餘下二張為另一組相同數字。例：7C、7S、7D、KH、KS。如有兩者以上則比較三張相同牌的數字大小，為了避免打平的情況發生，則再需比較餘下一對牌的大小。
同花 (Flush) ：五張牌為相同花色。例：5D、AD、KD、7D、QD。如有兩者以上則比較最大的牌，其次再比較第二大的牌，以此類推。
順子 (Straight) ：五張連續數字的牌。例：TH、JD、QC、KD、AS。注意 A 也可以當作最小的牌接在 2 之後。
三條 (Three of a Kind) ：三張相同數字的牌。例：QS、QH、QC、2D、3C。如有兩者以上則比較三張相同牌之大小，為了避免打平的情況發生，再比較其餘最大的牌，以此類推。
兩對 (Two Pair) ：各有兩副兩張相同數字的牌。例：2C、2H、6C、6S、4D。如有兩者以上則比較數字最大的一對牌，如果相同則比較另一對。若兩對數字皆相同，則比較剩下那一支牌。
一對 (One Pair) ：有一對牌的數字相同。例：2C、2H、4H、QH、KD。如有兩者以上相同則先比較一對的數字大小，接著比較餘下最大的牌，以此類推。
散牌 (High Cards) ：與上述皆不成立的手牌。例：3H、7D、JD、QD、AC。若有兩者以上則先比較最大的牌，再比較第二大，以此類推。
John Anthony 每次和他的朋友打賭 5 歐元，但他總是賭輸，有時是因為他所認為自己的手牌比實際上來的低所導致，特別是當他拿到順子的時候。
為了讓他自己的牌技進步，John Anthony 創造了一個單人玩的牌戲，他先將牌洗均勻，然後拿出其中的 49 張牌攤開排成 7×7 的矩形。以下例來說明：
2C KC 3D 7S 7H 5D 6D
2H 7D 4H 4S TS 3H 8S
3S 5H AD 5S 6S 3C 9C
9S JC QC KD JH KS QS
6C 8H AC 2S 6H AH KH
TC AS 9H QD 7C 4C 8C
TH 2D JS 9D 8D 5C JD
這時，他檢查每一橫列 (從上到下)、每一直行 (由左至右) 以及兩條對角線 (先檢查從左上至右下，再檢查從左下至右上) ，這 16 組牌組中，John 試著挑出其中 5 張讓這 5 張變成最大的牌組 (在Texas Hold’em中)。現在，他正央求你寫一個程式來確認他所選出的牌是不是最大的。
莫西亞 (Murcia，西班牙東南部的城市) 的摩天大樓成長得非常快速。從 15 世紀起，巴洛克式的 Glorieta 大教堂的輪廓就映照在這地平線上，但現在，新的摩天大樓開始矗立在莫西亞的田野 (huerta) 中。
有些人認為如果眼睛從左往右依序掃過，你可以觀察到一個越來越高的天際線，但其他人不認為是這樣，他們認為是越來越低的。
當我們的眼從左至右掃過莫西亞的天際，我們可以看到 N 個建築物，每個建築物有它自己的寬與高，你必須觀察出這些建築物是遞增還是遞減的排列著。我們定義如果建築群的最長遞增子序列 (longest increasing subsequence, LIS) 不小於最長遞減子序列 (longest decreasing subsequence, LDS) ，我們就稱它為遞增排列；反之，則稱為遞減排列。而子序列 (subsequence) 為原本序列在相同順序下的子集合，建築群的子序列長度為子序列中所有建築的寬之和。
舉例來說，假設我們有六座建築，而它們的高分別為：10、100、50、30、80、10；寬依序是：50、10、10、15、20、10。這時我們可以得出一條包含 3 棟建築物的遞增序列 (註：高為 10、30、80 的建築物) 而它的長度和為 85，與一列包含 1 座建築的遞減序列 (註：高為 10 的建築物) 而它的長度和為 50 (當然這裡有一列含 4 棟建築的遞減序列，然而它的長度為 45)，所以在這組測試資料中，我們可以說它的天際線是遞增的，範例請參照下圖。
這是一個在古老的鐵幕時代，有關間諜以及反間諜的問題。
在自由世界的一個秘密情報局 CONTROL，必須與邪惡的國際組織 KAOS 對抗。為了將帳冊送至 CONTROL 在鐵幕的獨立機構中，特務 82 到特務 85 在東方快車 (Orient Express) 的車廂上，被神秘且邪惡的 KAOS 特工 Cirilo Krochanska 所暗殺。而你，Maxwell Smart，特務 86，必須搭上火車和特務 B-12 接觸，將加密的訊息「tnih sevig cilc thgir」傳給他，並且避免成為 Krochanska 手下第五位犧牲者！
但是，Krochanska 在哪裡呢？我們知道他總是用火車來旅行，通常在歐洲某些重要的車站上，而且他已經準備好馬上去他想到達的目的地。
（如果你做過一點點情報工作的話，你將會發現 Cirilo Krochanska 其實是 …）
歐洲鐵路網有數條路線所構成，每條路線有它的起訖車站，路線中還有數個中繼站均勻分布在路線中。舉例來說，如果我們列舉出車站 1 至車站 13 所有的車站，我們可以列出以下三條路線：
在每條路線中火車是雙向行進的，從某一站行進下一站的時間恆為 2 個小時。就像你所看到的，有些車站出現在不同路線上，我們稱呼它為「重點車站」，而其餘的稱呼為「次要車站」。我們相信 Krochanska 位在一個去其他地方都是最快的重點車站，尤其是，從他座落的重點車站到其他重點車站，行進時間的平均值會達到最小。你可以假設從一條路線切換到另一條路線不會耗時，你必須找出 Cirilo Krochanska 在哪裡。
在某些民主國家中，執政黨會重劃選區以便在下次選舉時對他們有利。每個選區選出一位代表，在兩黨制的政體中，每個地區選舉的票數只要高於對手即可。
某個國家被切割成 $N\times{N}$ 個正方形區域，這些區域將會被合併為 N 個選區，每個選區包含 N 個相連的區域，這代表著我們可以上、下、左、右，移動至選區內所有的區域。
假定執政黨為 A，在野黨為 B，從上一次的選舉中，我們可以知道每個區域的投票情況。現在給你兩個 $N\times{N}$ 的矩陣，第一個是政黨 A 的投票情況，第二個則是政黨 B 的投票情況，對於每個選區，我們將包含在內所有區域的票數取總和，這時總票數多的政黨將會贏得選舉，如果兩黨的票數一樣，則此選區不會被選出代表。
現在政黨 A 僱用你去計算出，在重劃選區的情況下，最大可能的代表數差。
給妳三個數字輸出中間的即可。
假設 $K_n$ 為 n 個節點的完全無向圖且 n 為偶數，換句話說，$K_n$ 中兩個點皆連通。你的任務就是去找出 $K_n$ 所有擴張樹最大數量，而且這些擴張樹之間皆沒有共同的邊。
我們將用一種二分法的方式去產生一個數列，先從如下的數列開始：
0
1
將此數列依照水平線做鏡射，接著上半部的數列前面加 0，下半部前面加 1，你將會得到如下數列：
00
01
11
10
重覆此步驟，會再一次得到下面 8 個數字所構成的數列：
000 0
001 1
011 3
010 2
110 6
111 7
101 5
100 4
這些 2 進位的數字的右側是其對應的數字。
而這些數列分別被稱為 1 位元、2 位元及 3 位元的格雷碼 (Reflected Gray Code，或稱為 Gray Code)，一個 n 位元的格雷碼由 $2^n$ 個不同的數字所組成，而此數列上的數字，和其所相鄰的數字都差一個位元。